更新

有一些基本問題。這個想法的前提是，每個測量設備的誤差將得到平衡，因此，如果有足夠的設備，平均值將大致保持準確。如果不是這樣，至少您將能夠注意到兩個設備之間的差異，並知道何時重新校準。對於某些類型的測量，這大致上是正確的，但對於其他類型的測量則不是。

第一個大問題是某些類型的測量設備將總是傾向於朝同一方向漂移。例如，如果您的設備將力與彈簧進行比較，則該彈簧會隨著時間的推移變得較弱，而不會疲勞，因此永遠不會更強，因此您的測量值都將沿相同方向漂移。在這裡，對來自多個設備的結果求平均值將無濟於事，並且您甚至都不會注意到誤差，因為彈簧將以大致相同的速率衰減。

另一個基本問題是，即使是進行測量如果錯誤是雙向的且是隨機的，則需要大量的設備才能從統計學上確信您的平均值很好。僅使用兩個或三個設備-所有錯誤都可能在同一方向上，因此您的平均值仍然是錯誤的。您將需要大量的測量設備才能獲得平均值的精度。

除了這兩個基本原理外，當值很重要時，還有很多實際原因需要使用經過校準的測量設備。一種是處理樣本以對其進行多次測量會花費更多時間，機器和/或處理，這增加了成本和損壞風險。另一個是，對於大多數受標準控制的工作，單位將相對於絕對值（通常是物理常數，但有時是偽像）定義，並且如果您的測量與該值無關，則無法確定別人會同意的。對於某些關鍵工作，每次測量後都需要追溯到政府確定的常數。

由於所有這些原因，使用一台定期校準的儀器來代替一堆精度未知的儀器並試圖獲得統計平均值幾乎總是更好。

基於在您進行編輯時，我想我知道您不希望完全避免校準，只是為了降低頻率並降低儀器超出規格範圍（但在校準期內）會導致儀器故障的風險。完成品。這是一個好點-根據儀器故障的頻率，控製過程故障的頻率以及有缺陷的產品的成本，可以對過程故障進行風險分析。基於這些因素，您可以添加兩台儀器，也許只有其中一台處於其指定的校準週期內，而第二台只是作為故障監視器。如果兩種儀器不同意，您將無法確定哪一種是正確的，但您至少會知道出了點問題並檢查校準。這個想法沒有什麼錯，儘管可能仍無法檢測到共模故障，但它可能有助於檢測一些突然的故障。另一方面，將兩台儀器都保持在校準期內可能不會對經濟造成太大影響（例如，不要縮短校準間隔），這樣您就可以對結果更有信心了。

從答案的長度和答案的數量中可以很容易地看出，這個話題並不容易。

第一部分：
如果我們定義了過程參數（$ p $）沒有被監視。過程參數的測量值（$ m $）始終包含不確定性（$ u $）。因此，讓我們陳述以下模型：

$ m = p + u $

每次校準的目的都是指定不確定性。嚴格地說，不確定性只能針對已經完成的校准進行指定。但是，一個非常合理的假設是不確定性不會發生很大變化。但是，它將隨著時間而改變。因此該模型將如下所示：

$ m = p + u（t）$

根據冗餘的實現方式，您提出的冗餘對不確定性有不同的影響。一種方法是使用一個相同類型的附加傳感器測量相同的過程參數（1）。另一種方法是使用不同的傳感器（2），或者甚至使用不同的傳感器（3）觀察不同的過程參數。

僅使用相同的傳感器觀察相同的參數很可能具有校準質量也會下降。由於降級的原因沒有改變，因此兩個傳感器信號都可能隨時間推移具有更高的不確定性。

其他兩個選項都有可能提出不確定性模型，從而無法進行校準

第二部分：
在任何情況下，誤差和不確定性之間存在顯著的差異 。如果有可能知道每次測量的誤差，就可以輕鬆地彌補這一誤差。
但是校準只能提供測量的不確定性。或者換句話說，圍繞校準將為您提供一個估計值，該估計值可以確定（通常）在所有測量的95％中，返回值將在真實值附近的指定間隔內。假設模型非常簡單，不確定性的下限。

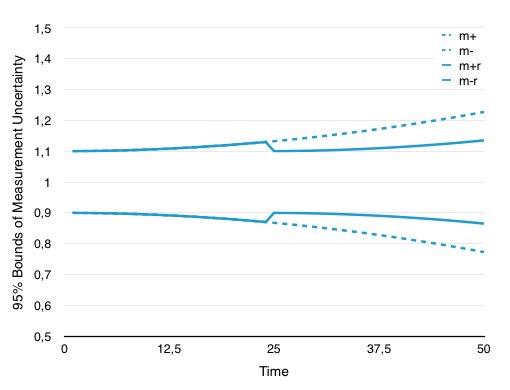
假設您希望將過程參數保持在“ 1”級別，並且不確定性的初始值為+/- 10％（雖然巨大，但可以更好地說明）。首先必須控制參數的原因是，您需要證明您的過程（或產品）具有特定的質量。在一段時間後，無需重新校準（界線m +和m-，點線）就可以很容易地看出，不確定性在不斷增加。通過在間隔的中間進行重新校準，可以減少不確定性（m + r和mr，固體）。

根據您的描述，我認為您需要在每個週期之前和之後報告或保存校準連同過程的測量日誌一起證明您整個生產週期的質量。

減少重新校準的工作量和相關成本是絕對可以理解的。唯一的方法是收集有關此特定過程的更多知識。
目前，蠻力方法是進行兩次校準，並假定兩次校準之間的不確定性在兩次校準之內。
如果有可能為不確定性降低獲得更好的模型，則可以減少校準次數。但是，為了擁有更好的模型，有必要結合大量的校準方法。一種可能的方法是使用所有可用的校準和重新校準。可能可以更好地了解不確定性，從而開發出更好的模型，從而延長校準間隔。

例如，假設傳感器將按照上圖所示的方式退化，則可以採用一種解決方案可能是隨著時間的推移更改生產系統控制的控制參數。但是，執行此操作的方法或什至可能執行此操作的方法在很大程度上取決於您尚不知道的過程。

最後，即使具有冗餘傳感器是違反直覺的，也不一定會降低不確定性。
通過向系統添加其他相同類型的傳感器，您基本上可以將測量數量加倍，從而保持相同的不確定性。冗餘傳感器降低不確定性的唯一方法是，當第一次傳感器測量值不能代表系統時，不僅傳感器具有不確定性，而且系統本身也會產生額外的波動。可以將測量視為對目標的射擊。根據您的技能，您將有一定的可能性擊中靶心。這意味著通過更頻繁地射擊，只會增加靶心，而不會減少射擊的傳播。每發子彈擊中靶心的可能性都相同。同樣，更頻繁地測量會增加測量“正確”值的機會，但這在此並不重要。有趣的是，您如何確定每個測量值都在正確值的某個“間隔內”。

總結一下：

1. 在測量中添加傳感器並不一定會降低組合測量的不確定性。

2. 與單個傳感器相比，具有兩個相同類型的傳感器不會改變組合測量值的降級率。

3. 如果可能性很大，在生產過程中，一個傳感器會返回錯誤的值，這比使用冗餘傳感器有意義。 但是，這與值的不確定性無關。在這種情況下，後校準將顯示由於傳感器故障而未對過程進行適當監控，因此根本沒有辦法確保生產運行的質量。如果出現傳感器故障，則另一個傳感器將插入並提供（至多）相同的質量，就像一個傳感器在整個生產過程中都可以倖存一樣。

4. 唯一的方法減少校準次數是為了收集過去的所有校準數據，並嘗試從中建立一個傳感器退化模型，這可能表明當前的校準數量不必要地高。

5. 通過使用不同的傳感器類型或過程參數的測量，可能會得出不確定性模型，該模型降級得更慢，並且在傳感器故障方面更可靠。

ol>

擁有兩個測量設備通常是避免重新校準的壞主意。如果設備給出不同的結果，您將不知道哪種方法正確，直到您重新校准或進行一些故障查找。當然，兩種不同的讀數告訴您某事是測量系統的錯誤，這不僅僅是一種錯誤的讀數，而是更多的信息。

如果您有 3 或更多設備，通常明智的做法是使用“多數表決”來確定一台設備正在提供不良數據，因此應將其忽略。

正如其他答案所述，您還需要考慮“共模”導致相同方式影響每個設備的錯誤原因-不僅是“不可控制”的事情，例如環境條件，還包括使用通用電源的問題，這些問題可能會超出規格而無任何指示，並影響所有設備的輸出

這始終是一個權衡。通常在經濟性和準確性之間。

如果您有兩個溫度記錄儀，並且其中一個掉落到校準範圍之外，但是您不知道是哪一個，則現在在溫度觀測上會有更大的不確定性。而且您要花兩倍的錢進行重新校準。

關於校準套件的好處是，在大多數情況下，這可以使您對觀察結果中的誤差分佈有一個非常合理的了解，並且使他們更容易解釋。擁有N位未校準的套件會使您對錯誤的實際分佈有很多不確定性，這使得管理和解決這些錯誤變得更加困難。因此，您有一個系統，在其中您為冗餘付出了額外的費用，但並沒有為降低的準確性進行補償。

如果您每次都要校準一個記錄器，而另一個記錄器不同時，您可以結束

，並且如果兩個記錄儀偏離校準，但彼此同步，那麼您將錯過一次重要的重新校準。而且，了解此類共模故障的分佈確實非常困難。因此，您將再一次沒有可以測量和管理的已知錯誤分佈；相反，您將獲得未知的錯誤分佈，這將增加您的成本。

更多具有相同精度的獨立測量只會改變錯誤的概率分佈，而不會改變最壞情況的錯誤。

一個很好的例子是滾動兩個骰子。您可以考慮將每個晶粒提供3.5±2.5的平均值。任何一個骰子的任何一個骰子都可以以相同的概率位於該範圍內的任何位置。但是，兩個骰子的平均值具有三角形輪廓。六個不同的可能組合得出3.5，而每個只有一個組合得出1或6。

滾動更多的骰子會使平均值的概率縮小到3.5左右，但是1或6的概率永遠不會變為0。最壞的情況仍然與以前相同。沒有任何多餘的骰子可以改變最壞的情況。

由於大多數時候都會進行生產測量，因此我們關心最壞的情況錯誤，多次測量無濟於事。

並且請注意，多個骰子的更好平均情況僅適用，因為每個度量（每個骰子）彼此獨立。即使是由不同的儀器獨立執行的同一測量過程也可能具有一些常見的誤差源。例如，溫度，大氣壓力，年齡等都會影響以相同方式測量同一物體的不同儀器。

很少有真正獨立的測量結果，然後才能得到更好的結果平均答案，反正不是更好的最壞情況。